Problem 1

For a matrix denoted by$M$, we write$M_{i: j, j k: l}$ for the submatrix formed from the rows$i$ through$j$ and the columns from$k$ through$l$ of the matrix. We also denote$M_{i: i, k: l}$ and$M_{i: j, k: k}$ by$M_{i, k: l}$ and$M_{i: j, k}$, respectively. (Note that they are row and column vectors, respectively.)

Assume below that$A$ is an$n \times n$ nonsingular matrix which can be LU factorized. In addition, assume that a positive integer$w$ exists such that all entries in the$k$-th sub- and super-diagonal of$A$ are zero if$k>w$. Namely, if$|i-j|>w, A_{i, j}$ is zero.

We denote the LU factorization of$A$ by$A=L U$, where$L$ is a lower triangular matrix with unit diagonal elements, and$U$ is an upper triangular matrix.

The following algorithm$\mathbf{P}$ computes$L$ and$U$ from the input$A$ in-place in such a way that the strictly lower triangular part and the upper triangular part of$A$ will be$L$ and$U$, respectively. In other words,$A_{i, j}$ will be$L_{i, j}$ for$i>j$, and$A_{i, j}$ will be$U_{i, j}$ for$i \leq j$, when it terminates.

Algorithm P

for(k=1 ; k<n ; k=k+1) {

$$\begin{aligned} A_{k+1: n, k} & \leftarrow \frac{1}{A_{k, k}} A_{k+1: n, k} ; \\ A_{k+1: n, k+1: n} & \leftarrow A_{k+1: n, k+1: n}-A_{k+1: n, k} A_{k, k+1: n} ; \end{aligned}$$

}

Answer the following questions.
(1) Compute the LU factorization of the following matrix.

$$\left(\begin{array}{cccc} 1 & 1 & 0 & 0 \\ -1 & 1 & 1 & 0 \\ 0 & -2 & 2 & 1 \\ 0 & 0 & -3 & 3 \end{array}\right)$$

(2) Prove that$L_{i, j}=0$ and$U_{i, j}=0$ if$|i-j|>w$.
(3) Assume that$n \gg 1, w \ll n$, and$m \gg n$. We wish to solve a set of linear systems,

$$A \vec{x}_{i}=\vec{b}_{i}, \quad i=1,2, \ldots, m$$

where$\vec{b}_{i}(i=1,2, \ldots, m)$ are the constant vectors, and$\vec{x}_{i}(i=1,2, \ldots, m)$ are the unknown vectors. Explain the relative merits of the following methods (I) and (II) with respect to the amount of arithmetic operations.

(I) Compute$A^{-1}$ first, and then compute each$\vec{x}_{i}$ as$A^{-1} \vec{b}_{i}$.

(II) Compute the LU factorization of$A$ first, and then solve$L \vec{y}_{i}=\vec{b}_{i}$ for$\vec{y}_{i}$. Solve$U \vec{x}_{i}=\vec{y}_{i}$ for$\vec{x}_{i}$ lastly.

Problem 2

Let$G=(V, E)$ be a simple undirected graph with the vertex set$V=\left\{v_{i} \mid i=1, \ldots, n\right\}$ and edge set$E$. For an$n$-dimensional vector$\boldsymbol{x}=\left(x_{1}, \ldots, x_{n}\right) \in\{-1,+1\}^{n}$, define$f_{G}(\boldsymbol{x})$ by

$$f_{G}(\boldsymbol{x})=\sum_{\left(v_{i}, v_{j}\right) \in E} \frac{1-x_{i} x_{j}}{2} .$$

Answer the following questions.

(1) For the case where$G$ is a complete graph$K_{n}$ of$n$ vertices, compute$\displaystyle a_{n}=\max _{\boldsymbol{x} \in\{-1,+1\}^{n}} f_{G}(\boldsymbol{x})$.

(2) Let$K_{n}$ and$a_{n}$ be those given in question (1). Let$b_{n}$ be the number of edges of$K_{n}$. Compute$\displaystyle \lim _{n \rightarrow \infty} \frac{a_{n}}{b_{n}}$.

(3) Let$G$ be an arbitrary simple undirected graph. When each$x_{i}$ takes a value of either$-1$ or$+1$ with probability$\displaystyle \frac{1}{2}$ independently, compute the expected value of$\displaystyle f_{G}(\boldsymbol{x})$. You may use the linearity of expectation.

(4) Show that, for any simple undirected graph$G$, there exists some$x \in\{-1,+1\}^{n}$ such that$\displaystyle f_{G}(\boldsymbol{x}) \geq \frac{|E|}{2}$. Here,$|E|$ denotes the number of edges of$G$.

Problem 3

Let$\boldsymbol{\Sigma}=\{a, b\}$. Answer the following questions.

(1) Give a non-deterministic finite state automaton with 3 states that accepts the following language.

$$\left\{w b a \mid w \in \Sigma^{*}\right\}$$

(2) Show the minimal deterministic finite state automaton that accepts the language given in question (1).

(3) Prove that the following language$L$ over$\Sigma$ is not regular. You may use the pumping lemma for regular languages.

$$L=\left\{w^{R} b a w \mid w \in \Sigma^{*}\right\}$$

Here,$w^{R}$ denotes the reverse of$w$. For example,$(a b b)^{R}=b b a$.

(4) Is the language$L$ in question (3) a context-free language? If it is, construct a context-free grammar that generates$L$. If not, prove that$L$ is not a context-free language.

Problem 4

Answer the following questions on digital circuits.
(1) Provide a Boolean expression of the output D according to the following truth table. Design and depict a corresponding combinational circuit by using at most six 2-input NAND gates.

Truth table

(2) Depict the internal structure of a D-flip-flop, and explain how the D-flip-flop holds a 1-bit value.

(3) Consider a clock-synchronous sequential circuit with a 1-bit input CLK, a 1-bit input$\mathbf{X}$, and a 1-bit output Y, where the input CLK is used for the clocking. The output Y is ‘1’ when the number of ’ 1 ’ in the input$\mathrm{X}$ values in the past three clock cycles (excluding the current clock cycle) is greater than the number of ’ 0 '. Otherwise, the output$Y$ is ’ 0 '. The output$\mathrm{Y}$ may be any value during the initial three clock cycles after the circuit is powered on. Assume that the circuit satisfies the setup-time and hold-time constraints. Design and depict the circuit. You may use at most two D-flip-flops and an arbitrary number of 2-input AND gates, 2-input OR gates, and NOT gates, if necessary.

2022 Summer CS

問题 1

オペレーティンク゚システムに関して以下の問いに答えよ.

(1) 5つのプロセス$P_{0}, P_{1}, P_{2}, P_{3}, P_{4}$ に対するスケジューリングについて, 各プロセス$P_{i}$ の到㖖 時間$(\mathrm{ms})$ と処理時間$(\mathrm{ms})$ をそれぞ$A_{i}$ と$C_{i}$ で表すすのとする. また, 同時に実行可能 なプロセスは 1 つのみで, コンテキストスイッチのオーバーへッドは無視できるものとする.$A_{0}=35, A_{1}=A_{2}=A_{3}=25, A_{4}=0, C_{0}=10, C_{1}=15, C_{2}=20, C_{3}=30, C_{4}=50$ である 場合に，5つのプロセスを Preemptive Shortest Job Firstアルゴリズムでスケジュールしたと きの平均ターンアラウンド時間と平均応答時間を求めよ. ここで, ターンアラウンド時間とは プロセスの到着から実行完了までの時間とし，応答時間とはプロセスの到着から実行開始まで の時間とする.

(2) 問い (1) と同じ到着時間と処理時間をもつ5つのプロセスを Non-Preemptive Shortest Job First アルゴリズム゙スケジュールしたときの平均ターンアラウンド時間と平均応答時間を求めよ.

(3) 問い (1) と同じ到着時間と処理時間をもつ5つのプロセスをタイムスライスが$10 \mathrm{~ms}$ の Round Robin アルゴリズムでスケジュールしたときの平均ターンアラウンド時間と平均応答時間を求 めよ. プロセスがタイムスライスを使い切らなかった場合は即座に次のプロセスのタイムスラ イスが開始されるすのとする. また, 新たに到着したプロセスは Round Robin キューの末尾 に追加されるものとし, 桵数のプロセスが同時にキューの末尾に到着した場合には残りの処理 時間の短いプロセスの方が優先されて追加されるものとする.

(4) 現実のオペレーティングシステムてはコンテキストスイッチのオーバーヘッドは無視できない. このオーバーヘッドを考慮した場合, Round Robin アルゴリスムの利点と欠点について CPU スケジューリングとメモリ管理の観点から説明せよ.

(5) 現実のオペレーティングシステムではプロセス侁先度を決定するためにしばしば Aging 方式が 使われる. Aging 方式の基本概念と古典的な静的佽先度方式に対する優位性について説明せよ.

Problem 1

Answer the following questions on operating systems.

(1) For the scheduling of five processes$P_{0}, P_{1}, P_{2}, P_{3}$, and$P_{4}$, the arrival time (ms) and the computation time$(\mathrm{ms})$ of each process$P_{i}$ are denoted by$A_{i}$ and$C_{i}$, respectively. Also, assume that only one process is allowed to execute at any instant, and the overhead of context switches can be ignored. Obtain the average turnaround time and the average response time when the five processes are scheduled by the Preemptive Shortest Job First algorithm, where$A_{0}=35, A_{1}=A_{2}=A_{3}=25, A_{4}=0, C_{0}=10, C_{1}=15, C_{2}=20, C_{3}=30$, and$C_{4}=50$. Here, the turnaround time refers to the time interval from the arrival of the process to the completion of its execution, and the response time refers to the time interval from the arrival of the process to the beginning of its execution.

(2) Obtain the average turnaround time and the average response time when the five processes with the same arrival and computation times as those given in question (1) are scheduled by the Non-Preemptive Shortest Job First algorithm.

(3) Obtain the average turnaround time and the average response time when the five processes with the same arrival and computation times as those given in question (1) are scheduled by the Round Robin algorithm with the time slice$10 \mathrm{~ms}$. The next time slice starts immediately when the current process does not exhaust its time slice. Also, a new process is added to the end of the Round Robin queue upon its arrival, and ties are broken in favor of the processes with shorter remaining computation times if multiple processes arrive at the end of the queue simultaneously.

(4) In real-world operating systems, the overhead of context switches cannot be ignored. Explain the pros and cons of the Round Robin algorithm from the viewpoint of CPU scheduling and memory management, when this overhead is considered.

(5) The Aging scheme is often used to determine process priorities in real-world operating systems. Explain the basic concept of the Aging scheme and its advantage over the classical static-priority scheme.

問题 2

C言語で書かれた以下のプログラムは整数配列 aの a[i] から a[j-1] までを昇順に整列する関数 mysort(a,i,j) を定義している$(i<j)$. プロクララム中の関数 multfrac(k,1,m) は$\mathrm{k}, 1, \mathrm{~m}$ が 正の整数であるとき$\displaystyle \mathrm{k} \times \frac{1}{\mathrm{~m}}$ 以上の最小の整数を求める関数であり,$\mathbf{w}, \mathbf{x}, \mathrm{y}, \mathbf{z}$は正の整数定数とする. 整の数の演算はオーバーフローしないすのとする.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

int multfrac(int k, int l, int m){
    return (k * l + (m - 1))/m;
}

void campare_swap(int *p, int *q){
    if (*p > *q){
        int tmp = *p;
        *p = *q;
        *q = tmp;
    }
}

void mysort(int a[],int i,int j){
    int k -j -i ;
    if (k < 4){
        /************
        *     X     *
        ************/
    }
    else {
        mysort(a, i, i + multfrac(k, x, w));
        mysort(a, j - multfrac{k, y, w}, j);
        mysort(a, i, i + multfrac(k, z, w));
    }
    
}

以下の問いに答えよ.

（1）(w, x, y, z) が$(4,3,3,3)$ である場合, 空欄$\mathrm{X}$ に入れるべき適切なコードを答えよ. た だし, comparo_orap 以外の関数呼び出しは不可とする. なお，コードは複数行にわたっても 良い.

(2) mysort(a, 0, n) が呼び出された時にコード断片$\mathrm{X}$ が実行される回数の合㖕を$T(n)$ と 表記する. が$(\mathbf{w}, \mathbf{x}, \mathrm{y}, \mathbf{z})$$(4,3,3,3)$ である場合,$T(n)$ の$n$ に関するオーダーを与えよ.

(3) (w, x, y, z) が$(4,2,3,3),(4,3,2,3),(4,3,3,2),(4,2,3,2)$ である場合のそれぞれについ て, mysort が常に正しく動作するか否かを答えよ.

(4)mysort が常に正しく動作するために w,$x, y, z$ が満たすべき必要十分条件を答えよ.

Problem 2

The following program written in C language defines a function mysort (a, i, j), which sorts an integer array a from a[i] to a[j-1] in ascending order (where$i<j$ ). The function multfrac (k, 1, m) used in the program returns the least integer that is greater than or equal to$\displaystyle k \times \frac{1}{\mathrm{m}}$, when$\mathbf{k}$, 1 , and$m$ are positive integers. Assume that $\mathbf{w}, \mathbf{x}, \mathrm{y} $ and$\mathbf{z}$ are positive integer constants. Assume also that integer operations never overflow.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

int multfrac(int k, int l, int m){
    return (k * l + (m - 1))/m;
}

void campare_swap(int *p, int *q){
    if (*p > *q){
        int tmp = *p;
        *p = *q;
        *q = tmp;
    }
}

void mysort(int a[],int i,int j){
    int k -j -i ;
    if (k < 4){
        /************
        *     X     *
        ************/
    }
    else {
        mysort(a, i, i + multfrac(k, x, w));
        mysort(a, j - multfrac{k, y, w}, j);
        mysort(a, i, i + multfrac(k, z, w));
    }
    
}

(1) Answer appropriate code to fill the blank$\mathrm{X}$ when$(\mathbf{w}, \mathbf{x}, \mathrm{y}, \mathbf{z})$ is$(4,3,3,3)$. You are not allowed to use a function call except for compare_swap. The code may consist of multiple lines.

(2) Let$T(n)$ denote the number of times that the code fragment$\mathrm{X}$ is executed while mysort (a, 0, n) is called. Give the order of$T(n)$ on$n$ when$(\mathrm{w}, \mathrm{x}, \mathrm{y}, \mathrm{z})$ is$(4,3,3,3)$.

(3) Answer whether or not mysort always works correctly for each case where$(\mathbf{w}, \mathbf{x}, \mathrm{y}, \mathbf{z})$ is (4,$2,3,3),(4,3,2,3),(4,3,3,2)$, and$(4,2,3,2)$.

(4) Give a necessary and sufficient condition on$w, x, y$, and$z$ that guarantees mysort to always work correctly.

問题 3

$\Sigma_{1}=\{\mathrm{a}, \mathrm{b}\}, \Sigma_{2}=\{\mathrm{t}, \mathrm{f}\}$ とする. 語$w \in \Sigma_{1}^{*}$ について,$w$ の長さを$|w|$ と畵く.また, 空語（す なわち長さ0の語）を$\epsilon$ と茟く. 語$w \in \Sigma_{1}^{*}$ について, 関数$f_{w} \in \Sigma_{1}^{*} \rightarrow \Sigma_{2}^{*}$ を以下のように定義する.
$\begin{aligned} f_{w}\left(w^{\prime}\right)=\left\{x_{1} \cdots x_{\mid w^{\prime}}\left|\in \Sigma_{2}^{*}\right|\right.\\ & x_{i}= \begin{cases}\mathrm{t} & \text { if } w^{\prime}=u w v \text { for some } u, v \in \Sigma_{1}^{*} \text { such that }|u|=i-1 \\ \mathrm{f} &\text { otherwise }\end{cases} \\\left.\text { for each } i \in\left\{1, \ldots,\left|w^{\prime}\right|\right\}\right\} . \end{aligned}$

すなわち,$f_{w}\left(w^{\prime}\right)$ は$w^{\prime}$ から,$w$ と一致する部分文字列の開始位䍛をたで置き換え, それ以外の位置 を$f$ で罩き換えて得られるものである. 例えば,$f_{a a}(\mathrm{baaab})=\operatorname{fttff}, f_{\epsilon}(\mathrm{abbab})=\operatorname{ttttt}$ である. さらに, 関数$f_{w}$ を，以下の定義によって$\Sigma_{1}$ 上の言語を$\Sigma_{2}$ 上の言語に写像する関数$f_{w}^{*}$ に拡張する.

$$f_{w}^{*}(L)=\left\{f_{w}\left(w^{\prime}\right) \mid w^{\prime} \in L\right\} .$$

例えば,$f_{\mathrm{ab}}^{*}\left(\left\{(\mathrm{abb})^{n} \mid n \geq 0\right\}\right)=\left\{(\mathrm{tff})^{n} \mid n \geq 0\right\}$ である.

以下の問いに答えよ.

(1)$f_{\text {aba}}$ (babababa) を求めよ.

(2)$f_{\mathrm{aba}}^{*}\left(\Sigma_{1}^{*}\right)$ を正規表現を用いて表せ.

(3) 語$w \in \Sigma_{1}^{*}$ (ただし$\left.|w|>0\right)$ および決定性有限オートマトン$\mathcal{A}=\left(Q, \Sigma_{1}, \delta, q_{0}, F\right.$ ) が与えられた とし,$\mathcal{A}$ が受理する言語を$L$ とする. ただし$Q, \delta, q_{0}, F$ は, それぞれ$\mathcal{A}$ の状態集合, 邉移関 数, 初期状態, 受理状培の集合を表すすのとし, 邉移関数$\delta \in Q \times \Sigma_{1} \rightarrow Q$ は全域関数である とする.$f_{w}^{*}(L)$ を受理する非決定性有限オートマトンを, 䉍単な説明ととすに与えよ.$\epsilon$ 哄移 を用いてもよい.

(4) 以下の命題が真ならばその証明の概賂（$f_{w}^{*}(L)$ を受理するプッシュダウンオートマトンまたは$f_{w}^{*}(L)$ を生成する文脈自由文法を简単な説明とともに示せばよい）を, 偽ならば反例を示せ. 命頙 :「すべての語$w \in \Sigma_{1}^{*}$ について,$L \subseteq \Sigma_{1}^{*}$ が文脈自由言語ならば,$f_{w}^{*}(L)$ も文脈自由言語 である」

Problem 3

Let$\Sigma_{1}=\{\mathrm{a}, \mathrm{b}\}$ and$\Sigma_{2}=\{\mathrm{t}, f\}$. For a word$w \in \Sigma_{1}^{*}$, we write$|w|$ for the length of$w$. We also write$\epsilon$ for the empty word (i.e., the word of length 0). For a word$w \in \Sigma_{1}^{*}$, we define the function$f_{w} \in \Sigma_{1}^{*} \rightarrow \Sigma_{2}^{*}$ by:

$$\begin{aligned} f_{w}\left(w^{\prime}\right)=\left\{x_{1} \cdots x_{\left|w^{\prime}\right|} \in \Sigma_{2}^{*} \mid\right.\\ & x_{i}= \begin{cases}t & \text { if } w^{\prime}=u w v \text { for some } u, v \in \Sigma_{1}^{*} \text { such that }|u|=i-1 \\ f &\text { otherwise }\end{cases} \\ &\text { for each } \left.i \in\left\{1, \ldots,\left|w^{\prime}\right|\right\}\right\} . \end{aligned}$$

In other words,$f_{w}\left(w^{\prime}\right)$ is the word obtained from$w^{\prime}$ by replacing the start position of each subword that matches$w$ with$t$ and any other position with$f$. For example,$f_{a a}($ baaab$)=$ fttff and$f_{\epsilon}($ abbab$)=$ ttttt. Furthermore, we extend the function$f_{w}$ to the function$f_{w}^{*}$ that maps a language over$\Sigma_{1}$ to a language over$\Sigma_{2}$ by the following definition:

$$f_{w}^{*}(L)=\left\{f_{w}\left(w^{\prime}\right) \mid w^{\prime} \in L\right\} .$$

For example,$f_{\mathrm{ab}}^{*}\left(\left\{(\mathrm{abb})^{n} \mid n \geq 0\right\}\right)=\left\{(\operatorname{tff})^{n} \mid n \geq 0\right\}$.
Answer the following questions.

(1) Compute$f_{\text {aba }}$ (babababa).

(2) Express$f_{\mathrm{aba}}^{*}\left(\Sigma_{1}^{*}\right)$ by using a regular expression.

(3) Suppose that a word$w \in \Sigma_{1}^{*}$ (where$|w|>0$ ) and a deterministic finite automaton$\mathcal{A}=$$\left(Q, \Sigma_{1}, \delta, q_{0}, F\right)$ are given, and that$L$ is the language accepted by$\mathcal{A}$. Here,$Q, \delta, q_{0}, F$ are respectively the set of states, the transition function, the initial state, and the set of accepting states of$\mathcal{A}$. Assume that the transition function$\delta \in Q \times \Sigma_{1} \rightarrow Q$ is total. Give a nondeterministic finite automaton that accepts$f_{w}^{*}(L)$, with a brief explanation. You may use$\epsilon$-transitions.

(4) If the following proposition is true, then give a proof sketch (it suffices to show a pushdown automaton that accepts$f_{w}^{*}(L)$ or a context-free grammar that generates$f_{w}^{*}(L)$, with a brief explanation). Otherwise, give a counterexample.

Proposition: “For every word$w \in \Sigma_{1}^{*}$, if$L \subseteq \Sigma_{1}^{*}$ is a context-free language, then$f_{w}^{*}(L)$ is also a context-free language.”

問题 4

コンピュータアーキテクチャに関する以下の問いに答えよ.

(1) 命令$i$ が生成する結果を命令$j$ が利用する可能性がある場合に, 命令$i$ に対する命令$j$ のデタ 依存が存在するといい,$j \rightarrow i$ と表す. 以下のプログラムに存在するデータ依存をすべて示せ. 各命令の動作はプログラム中のコメント（#以降の記述）の通りである. プログラムを実行す るプロセッサは x0 から x31 までの 32 個のレジスタを持ち, x0 は常に 0 を保持するゼロレジ スタとする. コメント中, メモリの addr 番地へのアクセスを “memory [addr]" と表す.

1
2
3
4
5
6
7
8

命令 0)       addi x3, x0, 64     # x3 <- x0 + 64
命令 1)       addi x4, x0, 0      # x4 <- x0 + 0
命令 2)       addi x5, x0, 0      # x5 <- x0 + 0
命令 3) Loop: lw x6, 0 (x4)       # x6 <- memory [x4 + 0]
命令 4)       add x5, x5, x6      # x5 <- x5 + x6
命令 5)       addi x4, x4, 4      # x4<-x4 + 4
命令 6)       blt x4, x3, Loop    # if x4 x3, goto Loop
命令 7)       sw x5, 4096(x0)     # memory[x0 + 4096] <- x5

(2) 每クロックサイクハ最大 1 命令を発行する, 5 段ステージのパイプラインプロセッサを考える. このプロセッサは, 命令フェッチ (IF) ステージ, 命令テコードとVジスタフェッチ (ID) ステー ジ, 実行 (EX) ステーシ, メモリアクセス (MA) ステージ, Vジスタ書き込み (WB) ステー ジの 5つのステージて棤成される. 各レジスタのピット幅は 32 である. 1 クロックサイクルて アクセス可能な命令メモリとデータメモリを持つすのとし, ロードワード命令 lw おびスト フワード命令 sw$ が MA ステージでストールすることはない. 命令 lw に関する被ロード・デー タハザードが発生する場合, IF ステージ, IDステージ，EXステージを1クロックサイクル するまで, IF ステージおよびID ステージをストールさせる. つまり, 分岐命令のフェッチ後, 2クロックサイクルの間, 後続の命令をフェッチしない，EXステージでの実行結果およびMA ステージでのロード結果は, EXステージに適切にフォワーデンングされるものとする.

被ロード・データハザードとは何かを説明せよ．また, このプロセッサ上て間い (1) のプログ ラムを実行する際に, 被ロード・゙゙ータハザードがとのように発生するかを説明せよ.

被ロード・データハザードとは何かを説明せよ. また, このプロセッサ上て問い (1) のプログ ラムを実行する際に，被ロード・データハザードがどのように発生するかを説明せよ.

(3) 問い (2) のプロセッサ上で, 問い (1) のプログラムを実行する際に要するクロックサイクル数 を求めよ. また, 平均 IPC (instructions per cycle) を小数第 2 位まで求めよ.

（4）問い (1) のプログラムおよび問い (2) のプロセッサを例に，動的分岐予測の原理と役割を説明 せよ.

Problem 4

Answer the following questions on computer architecture.

(1) When the instruction$j$ may use the result generated by the instruction$i$, we say there is a data dependency from the instruction$j$ to the instruction$i$, and write$j \rightarrow i$. Give all data dependencies in the program below. The behavior of each instruction is described as a comment (the description after #) in the program. The processor which executes the program has 32 registers from$x 0$ to$x 31$, and$x 0$ is the zero register that always keeps the value 0 . In the comment, we represent a memory access to the address addr on the memory as “memory [addr]”.

1
2
3
4
5
6
7
8

instruction 0)       addi x3, x0, 64     # x3 <- x0 + 64
instruction 1)       addi x4, x0, 0      # x4 <- x0 + 0
instruction 2)       addi x5, x0, 0      # x5 <- x0 + 0
instruction 3) Loop: lw x6, 0 (x4)       # x6 <- memory [x4 + 0]
instruction 4)       add x5, x5, x6      # x5 <- x5 + x6
instruction 5)       addi x4, x4, 4      # x4<-x4 + 4
instruction 6)       blt x4, x3, Loop    # if x4 x3, goto Loop
instruction 7)       sw x5, 4096(x0)     # memory[x0 + 4096] <- x5

(2) Consider a 5-stage pipeline processor that issues up to one instruction per clock cycle. The processor consists of 5 stages: instruction fetch (IF) stage, instruction decode and register fetch (ID) stage, execution (EX) stage, memory access (MA) stage, and register write back (WB) stage. The bit width of each register is 32. The processor has the instruction and data memories that can be accessed in one clock cycle, and load-word lw and store-word sw instructions do not stall on the MA stage. If there is a load-use data hazard for lw instruction, the IF, ID, and EX stages are stalled for one clock cycle. The branch instruction blt (branch if less than) stalls the IF and ID stages until the branch result is determined in the EX stage. Thus, the processor does not fetch subsequent instructions for two clock cycles after a branch instruction is fetched. Execution results in the EX stage and load results in the MA stage are properly forwarded to the EX stage.

Explain what the load-use data hazard is. Explain also how load-use data hazards occur when the program in question (1) is executed on the processor.

(3) Calculate the number of clock cycles required for the execution of the program in question (1) on the processor in question (2). Calculate also the average IPC (instructions per cycle) up to two places of decimals.

(4) Using the program in question (1) and the processor in question (2) as an example, explain the mechanism and role of dynamic branch prediction.

2022 Math

問题1

以下の$x, y, z \in \mathbb{R}$ に関する複数の条件を考える.

$$\left\{\begin{array}{cc} 0<z-x y & <1 \\ 0<z-(x+y)^{2} & <-x y \end{array}\right.$$

$\Omega$ を上記の条件を満たす$z$ が一つでも存在するような点$(x, y)$ の集合とする.$\Omega$ は三次元デ カルト座標系において上記の条件を満たすような点$(x, y, z)$ の集合を$x y$ 平面上に正射影し た図形とも解釈できる. 以下の問いに答えよ.

(1)$\Omega$ を$x$ と$y$ に関する不等式で表現せよ.

(2) 集合$\Omega$ を$x y$ 平面上に図示せよ. 図形の境界が$x$ 軸,$y$ 軸と交わる場合は, その交点 の座標も明記せよ.

(3) 集合$\Omega$ の境界の湾曲した区間は, 単位円の複数の円弧をある線形変換行列$\mathbf{X}$ で変換 した図形になっている. このような Xを一つ求めよ. ただし, 単位円上の点$(1,0)$ は, 湾曲した区間の最も曲率の高い点に変換されなければならない.

(4) (3)で求めた X の行列式を求めよ.

(5)集合$\Omega$ の面積を求めよ. ただし, 図形を線形変換した場合の面積変化率は, その線形 変換行列の行列式の絶対值に等しいことを用いてもよい.

Problem 1

Consider the following multiple conditions on$x, y, z \in \mathbb{R}$.

$$\left\{\begin{array}{cc} 0<z-x y & <1 \\ 0<z-(x+y)^{2} & <-x y \end{array}\right.$$

Let$\Omega$ be the set of points$(x, y)$ for which at least one$z$ exists satisfying the above conditions. Note that the set$\Omega$ can be seen in the three-dimensional Cartesian coordinate system as the orthogonal projection of points$(x, y, z)$ satisfying the above conditions onto the$x y$-plane. Answer the following questions.

(1) Find the inequalities on$x$ and$y$ representing$\Omega$.

(2) Draw a figure of$\Omega$ in the$x y$-plane. If the boundary of$\Omega$ intersects with the$x$-axis or the$y$-axis, write down the coordinates at each intersection.

(3) The curved segments of the boundary of$\Omega$ correspond to the linear transformation of arcs of the unit circle with a matrix$\mathbf{X}$. Find one such$\mathbf{X}$. Note that the point$(1,0)$ on the unit circle must be transformed to a point where the curvature is maximized in the curved segments.

(4) Calculate the determinant of$\mathbf{X}$ found in (3).

(5) Calculate the area of the set$\Omega$. Note that the absolute value of the determinant of a matrix is the area scale factor of the transformation with that matrix.

問题2

$\alpha \geq 1$ と$n>0$ に対し以下の積分$I_{n}(\alpha)$ を考える.

$$I_{n}(\alpha)=\int_{\frac{1}{n}}^{n} \frac{f(\alpha x)-f(x)}{x} \mathrm{~d} x$$

ただし， 実数值関数$f(x)$ は$x \geq 0$ において連続かつ微分可能で，導関数が連続であり,$\displaystyle \lim _{x \rightarrow \infty} f(x)=0$ が成り立つと仮定する. 以下の問いに答えよ.

(1)$\displaystyle J_{n}(\alpha)=\displaystyle \frac{\mathrm{d} I_{n}(\alpha)}{\mathrm{d} \alpha}$ とおく.$\displaystyle J_{n}(\alpha)=\frac{1}{\alpha}\left(f(\alpha n)-f\left(\frac{\alpha}{n}\right)\right)$ であることを示せ. ここでは, 積分と微分が交換可能であることを用いてよい.

(2)$\displaystyle I(\alpha)=\lim _{n \rightarrow \infty} I_{n}(\alpha)$ とおく. 任意の$\beta \in[1, \alpha]$ に対して$\displaystyle \lim _{n \rightarrow \infty} J_{n}(\beta)$ が存在し, かつ, これが$[1, \alpha]$ 上一様収束することを示し,

$$I(\alpha)=\int_{1}^{\alpha}\left(\lim _{n \rightarrow \infty} J_{n}(\beta)\right) \mathrm{d} \beta$$

であることを示せ.

(3)$I(\alpha)$ を求めよ.

(4) 以下の積分を求めよ. ただし,$p>q>0$ とする.

$$\int_{0}^{\infty} \frac{e^{-p x} \cos (p x)-e^{-q x} \cos (q x)}{x} \mathrm{~d} x$$

Problem 2

Consider the following integral$I_{n}(\alpha)$ for$\alpha \geq 1$ and$n>0$.

$$I_{n}(\alpha)=\int_{\frac{1}{n}}^{n} \frac{f(\alpha x)-f(x)}{x} \mathrm{~d} x$$

Assume that a real-valued function$f(x)$ is continuous and differentiable on$x \geq 0$, its derivative is continuous, and$\displaystyle \lim _{x \rightarrow \infty} f(x)=0$. Answer the following questions.

(1) Define$\displaystyle J_{n}(\alpha)=\frac{\mathrm{d} I_{n}(\alpha)}{\mathrm{d} \alpha}$. Show that$\displaystyle J_{n}(\alpha)=\frac{1}{\alpha}\left(f(\alpha n)-f\left(\frac{\alpha}{n}\right)\right)$.

You can use the fact that the integration and the differentiation commute in this context.

(2) Define$\displaystyle I(\alpha)=\lim _{n \rightarrow \infty} I_{n}(\alpha)$. Show that$\displaystyle \lim _{n \rightarrow \infty} J_{n}(\beta)$ exists for any$\displaystyle \beta \in[1, \alpha]$ and it uniformly converges on$[1, \alpha]$, and show that

$$I(\alpha)=\int_{1}^{\alpha}\left(\lim _{n \rightarrow \infty} J_{n}(\beta)\right) \mathrm{d} \beta .$$

(3) Obtain$I(\alpha)$.

(4) Calculate the following integral. Note that$p>q>0$.

$$\int_{0}^{\infty} \frac{e^{-p x} \cos (p x)-e^{-q x} \cos (q x)}{x} \mathrm{~d} x$$

問题3

$x y$ 平面上に,$0<x<1$ かつ$0<y<1$ で定義される領域$R$ を考える.$R$ 上にランダムに 1 点を選び, それを点$\mathrm{A}$ とする. ただし, 点$\mathrm{A}$ は$R$ 上に一様に分布するとする. 図に表すよ うに, 点$\mathrm{A}$ から$y$ 軸への垂線を$\mathrm{AB}$, 点$\mathrm{A}$ から$x$ 輣への垂線を$\mathrm{AC}$ とする. 原点を$\mathrm{O}$ とした とき, 長有形$\mathrm{OCAB}$ を「点$\mathrm{A}$ の長方形」と呼ぶ. また, 点$\mathrm{A}$ の長友形の面䅡を表す確率変 数を$S$ とする. 以下の問いに答えよ.

(1)$S$ の期待值を求めよ.

(2)$S \leq r$ となる確率を求めよ. ただし$0<r<1$ とする.

(3)$S$ の確率密度関数を求めよ.
再び, 領域$R$ を考える.$n$ を正の整数とする.$R$ 上にランダムに$n$ 点を選び, それらを点$\mathrm{A}_{1}, \mathrm{~A}_{2}, \ldots, \mathrm{A}_{n}$ とする. ただし, 各点は$R$ 上に一梂に分布し,$i \neq j$ である$\mathrm{A}_{i}$ と$\mathrm{A}_{j}$ は独立 に選ばれるとする. 次の問いに答えよ.

(4) 点$\mathrm{A}_{i}$ の長方形の面積を表す確率変数を$S_{i}$ とする.$Z$ を$S_{1}, S_{2}, \ldots, S_{n}$ の最小值を表 す確率変数とする. この時,$Z$ の確率密度関数を求めよ.

第 3 問

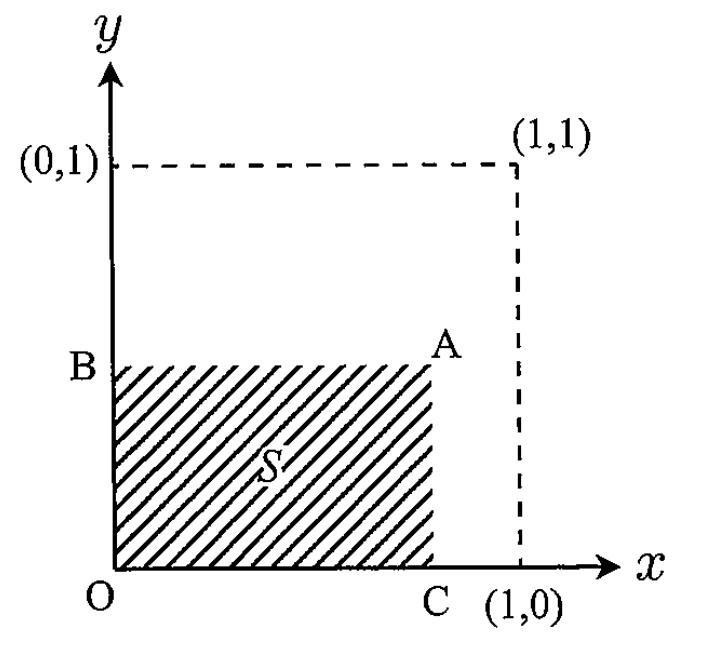
Problem 3

Consider a region$R$ defined by$0<x<1$ and$0<y<1$ in the$x y$-plane. We randomly select a point on$R$ and refer to the selected point as$\mathrm{A}$. We assume that$\mathrm{A}$ is uniformly distributed on$R$. Let$\mathrm{AB}$ be a perpendicular line from$\mathrm{A}$ to the$y$-axis and$\mathrm{AC}$ be a perpendicular line from A to the$x$-axis as shown in the figure. We call rectangle OCAB as "the rectangle of$\mathrm{A}$ ", where$\mathrm{O}$ denotes the origin. Let$S$ be a random variable representing the area of the rectangle of$\mathrm{A}$. Answer the following questions.

(1) Calculate the expectation value of$S$.

(2) Calculate the probability that$S \leq r$ holds, where$0<r<1$.

(3) Calculate the probability density function of$S$.
Again consider the region$R$. Let$n$ be a positive integer. We select$n$ points on$R$ and refer to the selected points as$A_{1}, A_{2}, \ldots, A_{n}$. We assume that each of the points is uniformly distributed on$R$, and$\mathrm{A}_{i}$ and$\mathrm{A}_{j}$ for$i \neq j$ are selected independently. Answer the following question.

(4) Let$S_{i}$ be a random variable representing the area of the rectangle of$\mathrm{A}_{i}$. Let$Z$ be a random variable which is the minimum of$S_{1}, S_{2}, \ldots, S_{n}$. Calculate the probability density function of$Z$.

Problem 3